第一章 传统词项逻辑
第一节 词项
词项充当直言命题的主项和谓项。“商品”这个词项的内涵是“用于交换的劳动产品”,外延是所有具体的商品。
单独词项(外延=1,如专有名词、“这本书”这样的限定摹状词)和普遍词项(外延>=2)
集合词项(“中国人是有骨气的”,这是“中国人”这个集合体的属性,未必每个个体都符合)和非集合词项(“中国人是亚洲人”,每个个体都符合)
一个词语可以表达不同词项(如上述“中国人”是两个不同词项),不同词语可以表达一个词项(如上述“中国人”也可以是“Chinese”)。
第二节 直言命题
直言命题=量项(所有/有的)+主项(S)+联项(是/不是)+谓项(P)
| 全称肯定(A) | 全称否定(E) |
| 单称肯定(I) | 单称否定(O) |
周延:词项的全部外延被断定。
如表格所示,上方二者(全称命题)主项周延,右方二者(否定命题)谓项周延。
SOP谓项周延的原因:“一些金属不是固体”,意味着金属中存在 a.是固体的金属 b.不是固体的金属,而命题断定了所有的固体都被不是 b.不是固体的金属。
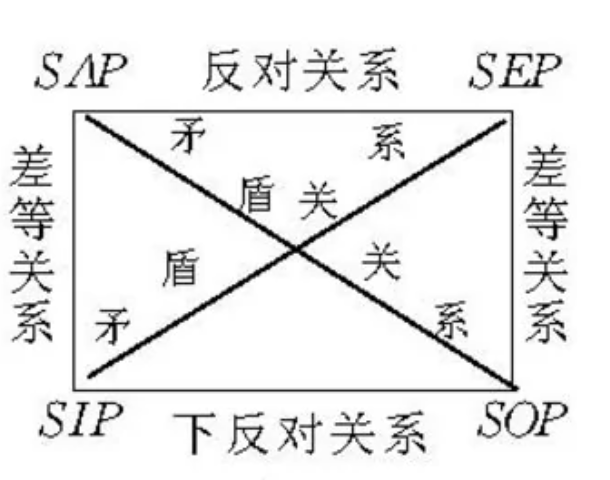
上图为对当方阵,表明四种命题间的真假关系。
上下真假相同,对角线真假相反,上方不能同真(一真另假),下方不能同假(一假另真)。
第三节 直接推理
分为对当关系推理,变形推理(换质推理/换位推理)。
换质推理和换位推理
换质推理:肯定否定互换,谓项换成补项(例:SAP├SE非P)。所有命题都能换质推理。补项的符号是上划线,“书”的补项可以称为“非书”。
换位推理:主项谓项互换,A变I,E和I不变,O不能换位(例:SAP├PIS)。
(简而言之,换质:A/E,I/O换,P→非P;换位:S/P换,A和I→I,E→E)
第四节 三段论
小项S,中项M,大项P(是S还是P根据结论来确定;前提中出现了P的是大前提,出现了S的是小前提,别根据前提的上下顺序判断;M在前提中出现两次,为S和P建立联系)
四条一般规则和两条导出规则
1.前提不周延,结论也不得周延(这是针对大小项而言的,因为中项一定会周延)
2.中项必须周延
3.两个前提不能同时否定
4.前提有否定命题,则结论是否定命题
导出1.两个前提不能同时特称
导出2.前提有特称命题,那么结论是特称命题
(简而言之,大小项结周则前周,中项必周;前不同否,前否结否;前不同特,前特结特)
三段论的格:第一格,M在左上右下;第二格,M在右右;第三格,M在左左;第四格,M在右左
第二章 命题逻辑
第一节 命题逻辑概述
句子有的没有真假(例如疑问句/感叹句等),有的有真假。有真假的句子表达的思想是命题,所以命题也有真假。
一个句子可以表达不同命题(如 a.下雨时说的“正在下雨” b.晴天时说的“正在下雨”),不同句子可以表达一个命题(如“正在下雨”和“It’s raining”)。
判断一个推理有效,就是在假定前提是真的时,必然能推出结论是真的。(也就是说推理过程是对的)
第二节 复合命题及其推理
复合命题的联结词也称为命题函数,即在联结词的空位上补充命题而得到复合命题的函数。y=f(x),填入命题x,就得到复合命题y。
在现代逻辑中,命题也叫公式。公式中可以使用括号消除歧义。
| 联结词 | 符号 | 术语 | 真值 |
| 并非 | 否定 | ¬ | A和¬A真假相反 |
| 并且 | 合取 | ∧ | AB同真,则A∧B真,否则假 |
| 或者 | 析取 | ∨ | AB同假,则A∨B假,否则真 |
| 如果…那么… | 蕴涵 | → | A假或B真,则A→B真,否则假 |
| …当且仅当… | 等值 | ←→ | AB相同,则A←→B真,否则假 |
蕴含命题的真值表
| A | B | A→B |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
“如果太阳从西方升起,那么1+1=2。”
“实质蕴涵怪论”是个难以理解的问题,这里直接背过就行。
可能的理解:
A是B的充分条件,意味着A真则B真,这只否定了A真而B假。也即:¬(A→B)←→(A∧¬B)
真命题和假命题不可同世而立,真命题在现实世界中同立。
